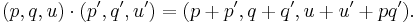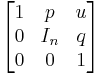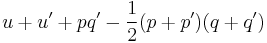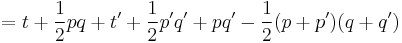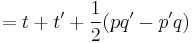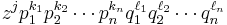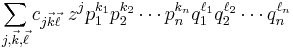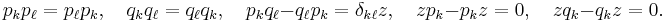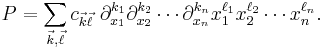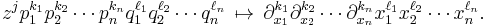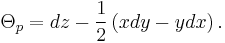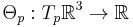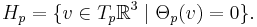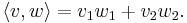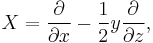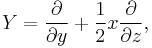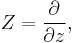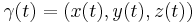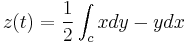Heisenberg group
In mathematics, the Heisenberg group, named after Werner Heisenberg, is the group of 3×3 upper triangular matrices of the form
or its generalizations under the operation of matrix multiplication. Elements a, b, c can be taken from some (arbitrary) commutative ring with identity, often taken to be the ring of real numbers or the ring of integers.
The real Heisenberg group arises in the description of one-dimensional quantum mechanical systems. More generally, one can consider groups associated to n-dimensional systems, and most generally, to any symplectic vector space.
Contents |
The three-dimensional case
There are several prominent examples of the three-dimensional case.
Continuous Heisenberg group
If a, b, c are real numbers (in the ring R) then one has the continuous Heisenberg group H3(R). It is a nilpotent Lie group.
In addition to the representation as real 3x3 matrices, the continuous Heisenberg group also has several different representations in terms of function spaces. By Stone–von Neumann theorem, there is a unique irreducible unitary representation of H in which its center acts by a given nontrivial character. This representation has several important realizations, or models. In the Schrödinger model, the Heisenberg group acts on the space of square integrable functions. In the theta representation, it acts on the space of holomorphic functions on the upper half-plane; it is so named for its connection with the theta functions.
Discrete Heisenberg group
If a, b, c are integers (in the ring Z) then one has the discrete Heisenberg group H3(Z). It is a non-abelian nilpotent group. It has two generators
and relations
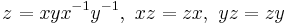 ,
,
where
is the generator of the center of H3. By Bass' theorem, it has a polynomial growth rate of order 4.
Heisenberg group modulo an odd prime p
If one takes a, b, c in Z/p Z for an odd prime p, then one has the Heisenberg group modulo p. It is a group of order p3 with two generators, x, y and relations
Analogues of Heisenberg groups over finite fields of odd prime order p are called extra special groups, or more properly, extra special groups of exponent p. More generally, if the derived subgroup of a group is contained in the center Z, of the group G, then the map from G/Z × G/Z → Z is a skew-symmetric bilinear operator on abelian groups. However, requiring that G/Z be a finite vector space requires the Frattini subgroup of G to be contained in the center, and requiring that Z be a one dimensional vector space over Z/pZ requires that Z have order p, so if G is not abelian, then G is extra special. If G is extra special but does not have exponent p, then the general construction below applied to the symplectic vector space G/Z does not yield a group isomorphic to G.
Heisenberg group modulo 2k
The Heisenberg group of order 8 is a dihedral group of order 8.
Observe that if
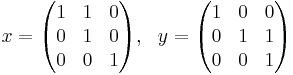 .
.
Then
and
Higher dimensions
More general Heisenberg groups 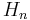 may be defined for higher dimensions in Euclidean space, and more generally on symplectic vector spaces. The simplest general case is the real Heisenberg group of dimension 2n+1, for any integer n ≥ 1. As a group of matrices, Hn (or Hn(R) to indicate this is the Heisenberg group over the ring R or real numbers) is defined as the group of square matrices of size n+2 with entries in R:
may be defined for higher dimensions in Euclidean space, and more generally on symplectic vector spaces. The simplest general case is the real Heisenberg group of dimension 2n+1, for any integer n ≥ 1. As a group of matrices, Hn (or Hn(R) to indicate this is the Heisenberg group over the ring R or real numbers) is defined as the group of square matrices of size n+2 with entries in R:
where a is a row vector of length n, b is a column vector of length n and 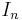 is the identity matrix of size n. This is indeed a group, as is shown by the multiplication:
is the identity matrix of size n. This is indeed a group, as is shown by the multiplication:
and
The Heisenberg group is a connected, simply-connected Lie group whose Lie algebra consists of matrices
where a is a row vector of length n, b is a column vector of length n and 0n is the zero matrix of size n. The exponential map is given by the following expression
By letting e1, ..., en be the canonical basis of Rn, and setting
the Lie algebra can also be characterized by the canonical commutation relations
where p1, ..., pn, q1, ..., qn, z are generators. In particular, z is a central element of the Heisenberg Lie algebra. Note that the Lie algebra of the Heisenberg group is nilpotent. The exponential map of a nilpotent Lie algebra is a diffeomorphism between the Lie algebra and the unique associated connected, simply-connected Lie group.
The above discussion (aside from statements referring to dimension and Lie group) applies if we replace R by any commutative ring A. The corresponding group is denoted Hn(A). Under the additional assumption that the prime 2 is invertible in the ring A the exponential map is also defined, since it reduces to a finite sum and has the form above (i.e. A could be a ring Z/pZ with an odd prime p or any field of characteristic 0).
On symplectic vector spaces
The general abstraction of a Heisenberg group is constructed from any symplectic vector space.[1] For example, let (V,ω) be a finite dimensional real symplectic vector space (so ω is a nondegenerate skew symmetric bilinear form on V). The Heisenberg group H(V) on (V,ω) (or simply V for brevity) is the set V×R endowed with the group law
The Heisenberg group is a central extension of the additive group V. Thus there is an exact sequence
Any symplectic vector space admits a Darboux basis {ej,fk}1 ≤ j,k ≤ n satisfying ω(ej,fk) = δjk and where 2n is the dimension of V (the dimension of V is necessarily even). In terms of this basis, every vector decomposes as
The qa and pa are canonically conjugate coordinates.
If {ej,fk}1 ≤ j,k ≤ n is a Darboux basis for V, then let {E} be a basis for R, and {ej,fk, E}1 ≤ j,k ≤ n is the corresponding basis for V×R. A vector in 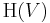 is then given by
is then given by
and the group law becomes
Because the underlying manifold of the Heisenberg group is a linear space, vectors in the Lie algebra can be canonically identified with vectors in the group. The Lie algebra of the Heisenberg group is given by the commutation relation
or written in terms of the Darboux basis
and all other commutators vanish.
It is also possible to define the group law in a different way but which yields a group isomorphic to the group we have just defined. To avoid confusion, we will use u instead of t, so a vector is given by
and the group law is
An element of the group :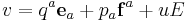 can then be expressed as a matrix
can then be expressed as a matrix
which gives a faithful matrix representation of H(V). The u in this formulation is related to t in our previous formulation by 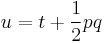 , so that the t value for the product comes to
, so that the t value for the product comes to
as before.
The isomorphism to the group using upper triangular matrices relies on the decomposition of V into a Darboux basis, which amounts to a choice of isomorphism V ≅ U ⊕ U*. Although the new group law yields a group isomorphic to the one given higher up, the group with this law is sometimes referred to as the polarized Heisenberg group as a reminder that this group law relies on a choice of basis (a choice of a Lagrangian subspace of V is a polarization).
To any Lie algebra, there is a unique connected, simply connected Lie group G. All other connected Lie groups with the same Lie algebra as G are of the form G/N where N is a central discrete group in G. In this case, the center of H(V) is R and the only discrete subgroups are isomorphic to Z. Thus H(V)/Z is another Lie group which shares this Lie algebra. Of note about this Lie group is that it admits no faithful finite dimensional representations; it is not isomorphic to any matrix group. It does however have a well-known family of infinite-dimensional unitary representations.
The connection with the Weyl algebra
The Lie algebra 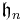 of the Heisenberg group was described above as a Lie algebra of matrices. The Poincaré–Birkhoff–Witt theorem applies to determine the universal enveloping algebra
of the Heisenberg group was described above as a Lie algebra of matrices. The Poincaré–Birkhoff–Witt theorem applies to determine the universal enveloping algebra 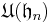 . Among other properties, the universal enveloping algebra is an associative algebra into which
. Among other properties, the universal enveloping algebra is an associative algebra into which 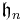 injectively imbeds. By Poincaré–Birkhoff–Witt, it is the free vector space generated by the monomials
injectively imbeds. By Poincaré–Birkhoff–Witt, it is the free vector space generated by the monomials
where the exponents are all non-negative. Thus 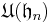 consists of real polynomials
consists of real polynomials
with the commutation relations
The algebra 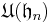 is closely related to the algebra of differential operators on Rn with polynomial coefficients, since any such operator has a unique representation in the form
is closely related to the algebra of differential operators on Rn with polynomial coefficients, since any such operator has a unique representation in the form
This algebra is called the Weyl algebra. It follows from abstract nonsense that the Weyl algebra Wn is a quotient of 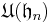 . However, this also easy to see directly from the above representations; viz. by the mapping
. However, this also easy to see directly from the above representations; viz. by the mapping
Representation theory
The representation theory of the Heisenberg group is fairly simple – later generalized by Mackey theory – and was the motivation for its introduction in quantum physics, as discussed below.
The key result is the Stone–von Neumann theorem, which, informally stated, says that (with certain technical assumptions) every representation of the Heisenberg group 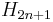 is equivalent to the position operators and momentum operators on Rn. Alternatively, that they are all equivalent to the Weyl algebra (or CCR algebra) on a symplectic space of dimension 2n.
is equivalent to the position operators and momentum operators on Rn. Alternatively, that they are all equivalent to the Weyl algebra (or CCR algebra) on a symplectic space of dimension 2n.
More formally, there is a unique (up to scale) non-trivial central strongly continuous unitary representation.
Further, as the Heisenberg group is a semidirect product, its representation theory can be studied in terms of ergodic theory, via ergodic actions of the group, as in the work of George Mackey.
Applications
Weyl's view of quantum mechanics
The application that led Hermann Weyl to an explicit introduction of the Heisenberg group was the question of why the Schrödinger picture and Heisenberg picture are physically equivalent. Abstractly, the reason is the Stone–von Neumann theorem: there is a unique unitary representation with given action of the central element z, up to a unitary equivalence: they are all equivalent to the position and momentum operators. Thus the Schrödinger picture and Heisenberg picture are equivalent – they are just different ways of realizing this unique representation.
Theta representation
The same uniqueness result was used by David Mumford for discrete Heisenberg groups, in his theory of equations defining abelian varieties. This is a large generalization of the approach used in Jacobi's elliptic functions, which is the case of the modulo 2 Heisenberg group, of order 8. The simplest case is the theta representation of the Heisenberg group, of which the discrete case gives the theta function.
Fourier analysis
The Heisenberg group also occurs in Fourier analysis, where it is used in some formulations of the Stone–von Neumann theorem. In this case, the Heisenberg group can be understood to act on the space of square integrable functions; the result is a representation of the Heisenberg groups sometimes called the Weyl representation.
As a sub-Riemannian manifold
The three-dimensional Heisenberg group H3(R) on the reals can also be understood to be a smooth manifold, and specifically, a simple example of a sub-Riemannian manifold.[2] Given a point p=(x,y,z) in R3, define a differential 1-form Θ at this point as
This one-form belongs to the cotangent bundle of R3; that is,
is a map on the tangent bundle. Let
It can be seen that H is a subbundle of the tangent bundle TR3. A cometric on H is given by projecting vectors to the two-dimensional space spanned by vectors in the x and y direction. That is, given vectors 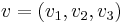 and
and 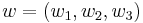 in TR3, the inner product is given by
in TR3, the inner product is given by
The resulting structure turns H into the manifold of the Heisenberg group. An orthonormal frame on the manifold is given by the Lie vector fields
which obey the relations [X,Y]=Z and [X,Z]=[Y,Z]=0. Being Lie vector fields, these form a left-invariant basis for the group action. The geodesics on the manifold are spirals, projecting down to circles in two dimensions. That is, if
is a geodesic curve, then the curve 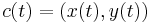 is an arc of a circle, and
is an arc of a circle, and
with the integral limited to the two-dimensional plane. That is, the height of the curve is proportional to the area of the circle subtended by the circular arc, which follows by Stokes' theorem.
See also
Notes
- ^ Hans Tilgner, "A class of solvable Lie groups and their relation to the canonical formalism", Annales de l'institut Henri Poincaré (A) Physique théorique, 13 no. 2 (1970), pp. 103-127.
- ^ Richard Montgomery, A Tour of Subriemannian Geometries, Their Geodesics and Applications (Mathematical Surveys and Monographs, Volume 91), (2002) American Mathematical Society, ISBN 0-8218-1391-9.
References
- Ernst Binz & Sonja Pods (2008) Geometry of Heisenberg Groups American Mathematical Society,ISBN 9780821844953.
- Hall, Brian C. (2004). Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. Berlin: Springer. ISBN 0387401229.
- Roger Evans Howe (1980) "On the role of the Heisenberg group in harmonic analysis", Bulletin of the American Mathematical Society 3(2):821.
- A.A. Kirilov (2004) Lectures on the Orbit Method, Chapter 2: "Representations and Orbits of the Heisenberg Group", American Mathematical Society.
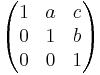
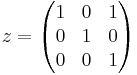
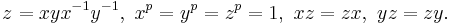
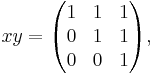
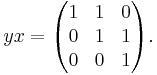
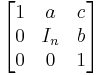
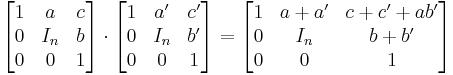
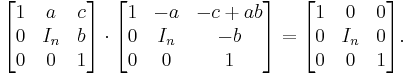
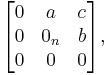
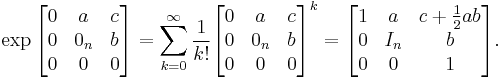
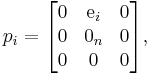
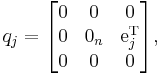
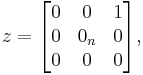
![[p_i, q_j] = \delta_{ij}z,](/2012-wikipedia_en_all_nopic_01_2012/I/7076a19aec1648c6f8b49e5ea9c40d3c.png)
![[p_i, z] = 0,](/2012-wikipedia_en_all_nopic_01_2012/I/43d7f04e067850b5d1c4bf4e307b5f74.png)
![[q_j, z] = 0,](/2012-wikipedia_en_all_nopic_01_2012/I/a1cd031664e2b326e8726d79268f2d55.png)
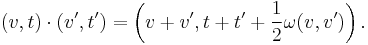
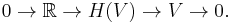
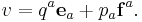
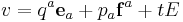
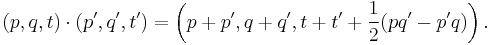
![[(v_1,t_1),(v_2,t_2)]=\omega(v_1,v_2)](/2012-wikipedia_en_all_nopic_01_2012/I/c6140d4c006154eb3c34393701299f86.png)
![[\mathbf{e}_a,\mathbf{f}^b]=\delta_a^b](/2012-wikipedia_en_all_nopic_01_2012/I/865d6d7ca3bd0caaa3bef4b7c2863384.png)